Определение условно-постоянной части текущих пассивов банка
Вожжов Анатолий Павлович
доктор экономических наук, профессор,
заведующий кафедрой финансов и кредита,
Луняков Олег Владимирович
доктор экономических наук, доцент,
профессор кафедры финансов и кредита,
Лунякова Наталья Автандиловна
кандидат экономических наук,
доцент кафедры финансов и кредита,
Институт финансов, экономики и управления,
Севастопольский государственный университет
Севастополь, Российская Федерация
Экономика региона
Т.12, Вып.1. 2016
В статье рассматриваются вопросы определения условно-постоянной части текущих пассивов банка. Целью статьи является разработка научно-методического подхода для определения условно-постоянной части текущих пассивов банка в условиях трудоемкости получения и обработки данных о факторах-детерминантах депозитов до востребования. В качестве основной гипотезы постулируется предположение о неоднородности дисперсии ежедневных совокупных остатков депозитов до востребования.
Анализ научно-методических подходов стабилизации текущих пассивов свидетельствует о необходимости дальнейшего совершенствования научного инструментария. В частности, предлагаемый рядом ученых коэффициентный анализ рассматривает в основном средние величины оборота средств по счетам, которые могут значительно изменяться на протяжении календарного года. Использование вероятностных законов распределения для определения ожидаемой величины неснижаемого остатка возможно лишь при «идеальных» финансовых условиях, когда не принимается во внимание влияние факторов на величину совокупных остатков средств до востребования. Разработанные статистические модели не учитывают возможную неоднородность дисперсии этих остатков.
В статье предложено использовать эконометрические методы, а именно, методы анализа временных рядов для проверки гипотезы о неоднородности дисперсии ежедневных совокупных остатков депозитов до востребования. В частности, проведена формализация, а также оценены параметры EGARCH-модели, которая позволяет учитывать нелинейные, асимметричные эффекты в колебаниях финансового ряда. На основе выявленных закономерностей предложен расчет определения условно-постоянной части депозитов до востребования.
Результаты исследований подтверждают гипотезу волатильности дисперсии совокупных остатков средств до востребования. Неравномерный характер их колебаний может быть следствием влияния шоков в экономике. Предложенный научно-методический подход может быть использован в процессе управления пассивами банка, как на микроуровне, так и на уровне региональной банковской сети.
Введение
Одной из наиболее значимых функций банковского сектора экономики является формирование кредитно-инвестиционных ресурсов. Качественное изменение параметров аккумулированных банком средств и приведение их в соответствие с требованиями кредитной, инвестиционной деятельности банка и поддержания требуемой ликвидности обеспечивается с помощью процессов трансформации банковских ресурсов [1, c. 16]. Под трансформацией в данном случае понимается совокупность приемов и способов такого комбинирования краткосрочных депозитов и займов, при котором существенная часть их совокупного объема образует постоянный, стабильный, или неснижаемый остаток [2, с. 24].
Трансформация банковских ресурсов проявляется как на микро-, так и на макроуровне: банки аккумулируют «короткие» и «маленькие» вклады, трансформируют их в «длинные» и «крупные» ресурсы и передают субъектам экономики для финансирования инвестиционной деятельности. В результате инвестиционно-кредитной мультипликации и прохождения денежных средств через потоки рыночной экономической системы долгосрочные ресурсы возвращаются в банковскую систему в трансформированном виде, в значительной мере в виде «коротких» и небольших по объемам депозитов до востребования.
Стабильность трансформации аккумулированных банковским сектором экономики средств в кредитно-инвестиционные ресурсы в процессе реализации банками своей посреднической функции зависит от соотношения и характера влияния внутренних и внешних факторов. При этом умелое научно обоснованное управление банковскими ресурсами должно обеспечивать, с одной стороны, способность банков своевременно выполнять обязательства перед своими вкладчиками и кредиторами, а с другой — приносить маржу, достаточную для развития банковского бизнеса.
Среди банковских ресурсов депозиты до востребования традиционно считаются наименее устойчивым видом ресурсов [3, с. 22]. Ежедневный остаток по каждому такому счету является случайной величиной, которая колеблется от нуля до некоторого максимума в зависимости от устойчивости ведения клиентом его хозяйственной деятельности, спроса на продукцию, которая им выпускается, или на оказываемые им услуги, активности проведения операций по счету, финансовой устойчивости клиента, а также зависит от количества клиентов, от уровня деловой активности в государстве и в конкретном регионе, в том числе сезонности.
Вместе с тем, в своей совокупности депозиты до востребования представляют собой довольно значительный по объему и относительно дешевый дополнительный банковский ресурс, который целесообразно трансформировать в «длинные» и «крупные» ресурсы.
Кроме того, в банковской практике считается неэффективной система управления активами, предусматривающая полное покрытие данных обязательств высоколиквидными активами [4, с. 17]. Обычно покрытием высоколиквидными активами обеспечивается только нестабильная часть депозитов до востребования. Поэтому важной задачей банковского менеджмента является определение условно-постоянной части депозитов до востребования, которая обеспечивала бы желаемое соотношение ликвидности и доходности.
Вопросы определения неснижаемой части депозитов до востребования и их использования в качестве ресурса для размещения в срочные активы исследовались в работах А.П. Вожжова [1, 2], Е.Б. Герасимовой [3], А.Т. Карчевой [5], П.В. Конюховского [6], О.И. Лаврушина [7], Ю.С. Масленченкова [8], Г.С. Пановой [9], К.Р. Тагирбекова [10], В.С. Сухарского [11], Ю. Толочко [4] и других ученых [12-14].
Научные изыскания и широкая дискуссия в банковском менеджменте относительно определения условно-постоянной части текущих пассивов позволяют судить об актуальности и практической значимости вопроса для банковского сектора, а необходимость эффективного управления финансами и денежным обращением, в свою очередь, требует развития теории банкинга, выявления фундаментальных закономерностей, определяющих формирование долгосрочных банковских ресурсов.
Классификация научно-методических подходов к определению уровня стабилизации текущих пассивов представлена на рисунке 1.
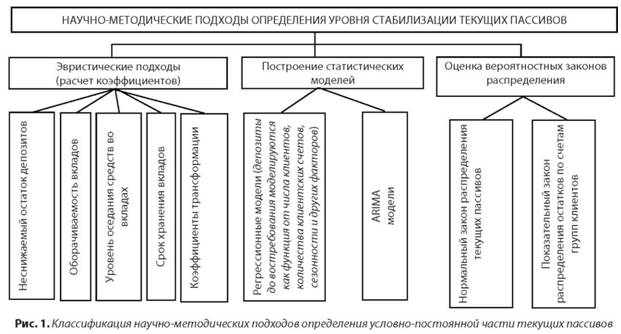
Эвристические подходы, основанные на расчете коэффициентов
Ученые К.Р. Тагирбеков, Г.С. Панова, О.И. Лаврушин, Р.И. Шиллер предложили производить расчет неснижаемого остатка депозитов до востребования:
Но = Оср / П х 100%, (1)
где Но — неснижаемый остаток депозитов до востребования;
Оср — средний остаток средств в течение периода;
П — поступления во вклады в течение периода (кредитовый оборот).
Следует отметить, что формула (1) не учитывает особенностей формирования неснижаемого остатка. В частности, в одних банках при относительно постоянной величине условно-постоянной части текущих пассивов наблюдаются различные диапазоны отклонений остатков. В других банках, наоборот, при различной условно-постоянной части наблюдаются одинаковые диапазоны отклонений. Использование в формуле среднего остатка обоснованно. Однако использование значений кредитового оборота с учетом указанных особенностей нелогично и не позволяет определить величину неснижаемого остатка.
Е.Б. Герасимова отмечает: «Наиболее близкой для определения неснижаемого остатка средств до востребования является величина минимального их остатка. Минимальный остаток за период определяется отдельно по каждой из выделенных групп клиентов по массиву ежедневных остатков, для сезонных клиентов — за последний квартал, для остальных — за полугодие. Суммирование этих минимальных значений будет представлять собой условную минимальную величину остатка на счетах до востребования банка за анализируемый период» [3, с. 23]. При этом автор раскрывает природу формирования минимального остатка, но не дает количественную оценку его определения.
В.С. Сухарский предложил рассчитывать оборачиваемость вкладов по формуле:
Оборачиваемость = оборот по приходу вкладов / среднемесячный остаток вкладов х 100 %. (2)
Формула (2) по входящим в нее составным элементам является обратной формуле (1) и также не отражает формирование неснижаемого остатка.
Г.С. Панова, О.И. Лаврушин, К.Р. Тагирбеков, Ю.С. Масленченков, В.С. Сухарский предложили рассчитывать уровень оседания средств:
Уо = (Ок - Он) / П х 100%, (3)
где УО — уровень оседания средств во вкладах;
Ок — остаток вкладов на конец периода;
Он — остаток вкладов на начало периода;
П — поступления во вклады.
Формула (3) отражает отношение прироста остатков во вкладах к кредитовому обороту, но не определяет величины неснижаемого остатка.
К.Р. Тагирбеков, Г.С. Панова, О.И. Лаврушин, Ю.С. Масленченков предложили еще один показатель, который можно использовать для стабилизации текущих пассивов, а именно, средний срок хранения вклада:
С = Оср х Д / В, (4)
где C — средний срок хранения средств на депозитах до востребования;
Оср — средний остаток средств в течение периода;
Д — количество дней в рассматриваемом периоде;
В — изъятие или перевод средств в течение периода (дебетовый оборот).
Формула (4) предусматривает определение срока хранения средств на счетах до востребования. Вместе с тем, она не показывает, будут ли средства только храниться или предусматривается также и их размещение. Срок, на который они могут быть размещены в активы, не определен.
В.С. Сухарский предложил несколько иную формулу для определения срока хранения вклада:
СТЗ = 360 / Оборачиваемость вкладов, (5)
где СТЗ — среднегодовой срок хранения одной денежной единицы (дней).
П.В. Конюховский, Г.С. Панова, О.И. Лаврушин предложили производить в расчет коэффициента трансформации:
K = (R – S) / S х 100%, (6)
где K — коэффициент трансформации краткосрочных ресурсов в долгосрочные, (используемый французскими банками);
R — краткосрочные ресурсы;
S — краткосрочные ссуды и вложения капитала.
Формула (6) отражает долю краткосрочных активов, финансируемых за счет краткосрочных ресурсов, но не определяет величины условно-постоянной части текущих пассивов и их трансформации.
П.В. Конюховский, Ю.С. Масленченков предложили рассчитывать коэффициент трансформации посредством применения дебетового и кредитового оборотов:
KT = 1 - ДОБ / КОБ , (7)
где КТ — коэффициент трансформации краткосрочных ресурсов в долгосрочные;
ДОБ — дебетовый оборот по выданным краткосрочным ссудам и другим краткосрочным вложениям (сроком до одного года);
КОБ — кредитовый оборот по поступлению средств на депозитные счета (сроком до 1 года).
Использование в формуле (7) значений дебетового и кредитового оборотов дает общее представление о процессе, показывает изменение неснижаемого остатка, но не определяет его величины и периода времени, на который ресурсы могут быть размещены в активы.
Для определения суммы потенциальных долгосрочных вложений Ю.С. Масленченков предложил следующий расчет:
М = (ЗН / КО - ЗК) х КО + ЗНД + КОД - ЗКД, (8)
где М — общая сумма ресурсов потенциальных долгосрочных вложений банка;
ЗН, ЗК — средства на счетах до востребования клиентов на начало и конец сравниваемых периодов деятельности;
КО — кредитовый оборот по поступлениям средств на счета до востребования клиента;
ЗНД, ЗКД — средства на счетах банка, предназначенные для кредитования и вложений сроком свыше 1 года соответственно на начало и конец сравниваемых периодов деятельности;
КОД — кредитовый оборот по поступлению на счета клиента средств, имеющих срочный характер.
В формуле (8) при определении потенциальных вложений банка в долгосрочные ресурсы речь идет о средствах до востребования и средствах, имеющих срочный характер, что не отражает технологии трансформации средств до востребования в текущие пассивы, в основе которой лежит возможность использования в качестве долгосрочных вложений части текущих пассивов банка.
На основе проведенного анализа можно сделать вывод, что вопрос оценки уровня трансформации текущих пассивов имеет существенное значение для банковской практики. Однако рассмотренные коэффициенты не только различаются, но даже в определенной мере противоречат друг другу.
Оценка вероятностных законов распределения
В ряде научных работ [1-2] произведены системные исследования по выявлению закономерностей формирования остатков средств как по отдельным текущим счетам, так и по текущим пассивам банка. По результатам исследований выявлены следующие особенности:
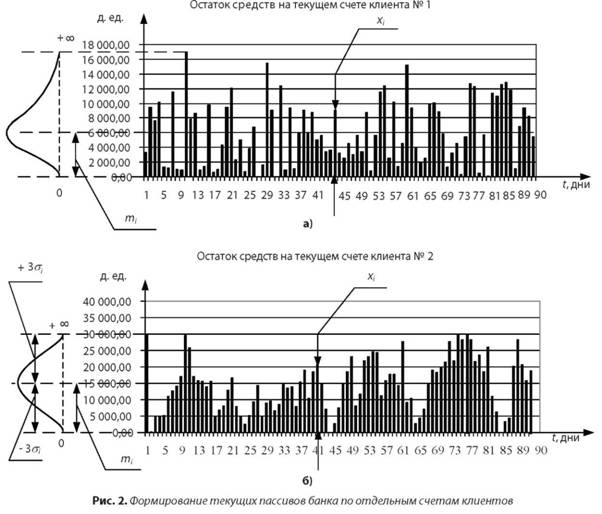
- При исключении влияния экзогенных факторов плотность вероятностей распределений величин остатков средств xi на счете на окончание каждого дня может соответствовать различным законам распределения: нормальному, экспоненциальному или равномерному со своим математическим ожиданием mi и стандартным отклонением σi (рис. 2).
- В качестве экзогенных факторов, оказывающих воздействие на динамику текущих пассивов, выступают количество клиентов, количество счетов, сезонность, спрос на продукцию клиентов и т. п.
- Формирование текущих пассивов происходит вследствие суммирования депозитов до востребования, при этом нестабильные остатки, изменяющиеся в диапазоне от нуля до их максимума накладываются друг на друга, создавая в результате неснижаемый остаток в виде условно-постоянной части текущих пассивов [2, с. 206].
- В идеальном случае, когда текущие пассивы в течение рассматриваемого периода не подвержены изменениям в силу сезонных отклонений, изменений пиковых оборотов по счетам и изменению количества клиентов на расчетно-кассовом обслуживании, на основании центральной предельной теоремы можно говорить о том, что распределение текущих пассивов как суммы всех отдельных текущих счетов приближается к нормальному закону распределения (рис. 3).
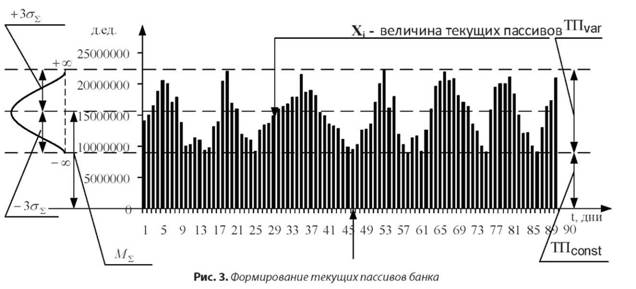
График, представленный на рисунке 3, схематично отражает формирование текущих пассивов банка, при этом их средняя величина М∑и диапазон отклонений +3σ∑остаются неизменными в рассматриваемом интервале времени. В составе текущих пассивов выделяются две части: условно-постоянная часть (ТПconst), которая в данном идеальном случае не изменяется, и переменная, варьирующая часть (ТПvar), так называемая мерцающая часть текущих пассивов.
В целях выявления фундаментальных закономерностей, а также определения количественных параметров формирования условно-постоянной части текущих пассивов предложено [2] рассматривать распределение текущих пассивов в классической форме в виде нормального закона распределения. Соответственно, величина условно-постоянной части текущих пассивов (ТПconst) определяется как разница между суммарным математическим ожиданием M∑ и возможным отклонением переменной части текущих пассивов в сторону уменьшения на величину 3σ∑ :
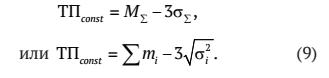
Если допустить, что по всем текущим счетам такие параметры как m. и а. одинаковы, то формула (9) принимает следующий вид:
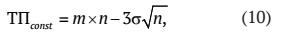
где m — средний остаток средств по каждому из текущих счетов;
σ — среднеквадратическое отклонение по каждому из n текущих счетов;
n — количество текущих счетов, обслуживаемых банком.
Из формулы (9) следует, что величина находится в прямой зависимости от количества обслуживаемых текущих счетов и средних величин их остатков.
Таким образом, определение условно-постоянной части депозитов до востребования на основе вероятностных моделей законов распределения возможно, но лишь при условии исключения влияния наиболее значимых факторов, рассмотренных выше. Отметим, что в ряде случаев выборка из фактических данных по текущим пассивам, в частности, депозитам до востребования, вполне может подчиняться нормальному закону распределения. Вместе с тем, такая выборка, представляющая временной ряд, может не иметь стационарного характера. Поэтому в данном случае определение условно-постоянной части на основе «подогнанного» закона распределения будет некорректно и может привести к росту потенциальных рисков ликвидности в процессе трансформации банковских средств в кредитно-инвестиционные ресурсы.
Построение статистических моделей
I. Регрессионные модели, в которых депозиты по востребования моделируются как функция от числа клиентов, количества клиентских счетов, сезонности и других факторов. Как показали исследования, проведенные по фактическим данным банковских учреждений, распределение ежедневных остатков депозитов до востребования имело лишь приближенное отношение к тому или иному закону распределения в силу влияния неучтенных факторов, которые оказывают существенное воздействие на формирование текущих пассивов.
Для решения данной проблемы А.Т. Карчева предложила подход к определению неснижаемого остатка текущих пассивов, который базируется на использовании аналитического тренда и дает возможность более точно определять инвестиционные возможности банков [5].
Последующие научные исследования в этом направлении [15] позволили специфицировать и оценить многофакторные регрессионные модели зависимости депозитов до востребования от ряда детерминант (сезонности, количества клиентов), в частности:
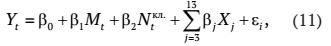
где Yt — уровень депозитов до востребования в момент времени t;
Mt — порядковые значения календарных месяцев (тренд);
Ntкл — среднемесячное количество клиентов;
Xj — сопутствующая переменная временного ряда;
β0, β1, β2 — регрессионные параметры;
βj — индексы сезонности;
j — порядковые номера месяцев в году;
εi — ошибка модели (с математическим ожиданием M(εi) = 0 и дисперсией σ2 (εi) = σ2).
В предположении нормальности распределения ошибки модели (εi), используя введенное ранее обозначение ТПconst, запишем выражение, которое на основе формулы (11), определят значение условно-постоянной части депозитов до востребования в периоде:
ТПconst(t) = Yt - 1,96σεi, (12)
где Yt, σεi — оцененные значения уровня депозитов до востребования и стандартного отклонения соответственно.
Использование в формуле (12) в качестве диапазона возможных отклонений величины 1,96σ вместо 3σ (формула (9)), по мнению авторов, является достаточно обоснованным в силу свойств плотности вероятности нормального закона распределения. Известно, что уровень достоверности (вероятности) попадания случайной величины X(εi) в интервал (M(x) &plusm; 1,96σ) составляет 95 % [16].
Рассматриваемый научно-методический подход учета комплекса факторов при определении условно-постоянной части депозитов до востребования, по сути, качественно дополняет чисто стохастические модели.
При этом заметим, что агрегирование данных по совокупным остаткам средств, количеству клиентов и их счетов на уровне календарных месяцев (формула (11)) позволило выявить существенные статистические взаимосвязи между уровнем депозитов до востребования и анализируемыми факторами и вполне может быть использовано в процессе прогнозирования и планирования банковской деятельности.
Также обращаем внимание на еще один аспект проблемы, который ранее авторами не рассматривался. Природа финансовых временных рядов, к которым относятся и депозиты до востребования, не исключает наличия нелинейного характера взаимосвязей между анализируемыми параметрами, причем дисперсия ошибки (8) может быть непостоянной. Кроме этого, возникает объективная необходимость в проверке гипотезы о наличии кластеров (пулов) в изменении остатков средств до востребования, когда большим отклонениям предшествуют высокие, а несущественным — незначительные отклонения.
Вследствие достаточно неравномерного характера изменения ежедневных остатков средств по клиентским счетам, наличия так называемых «интервенций» (резкого изменения средств на счете) [4, с. 18], свою актуальность приобретает вопрос выявления и оценки временных закономерностей по ежедневным (актуальным) остаткам депозитов до востребования.
II. Интегрированные модели авторегрессии скользящего среднего (ARIMA) можно использовать в условиях трудоемкости получения и обработки данных о факторах-детерминантах депозитов до востребования. Кроме этого, научно-методические подходы определения условно-постоянной части депозитов до востребования, основанные на использовании ARIMA-моделей, позволяют выявить временные закономерности изменения депозитов до востребования по их фактическим ежедневным остаткам.
В качестве примера использования ARIMA-моделей можно привести научные исследования Национального банка Республики Беларусь [4]. Для прогнозирования предполагаемого стабильного остатка средств на счете до востребования специалистами банка была предложена следующая схема исследования:
- Подбор наиболее подходящей ARIMA-модели, которая позволяет получить доверительные интервалы (с 85-процентной вероятностью) будущих значений остатков средств на счете до востребования. В результате была найдена наиболее адекватная модель прогнозирования (модель первых порядков авторегрессии с интегрированием ARIMA(1, 1, 0)) для описания фактических остатков средств на клиентском счете [4, с. 19].
- Анализ и оценка вероятности интервенций (внезапного значительного списания денежных средств), которые в финансовых исследованиях также получили название неординарных отклонений. В предположении о невысокой частоте существенных списаний средств со счета (в стабильных экономических условиях) была построена и оценена гистограмма их логнормального распределения. Принимая во внимание, что довольно существенные (неординарные) списания средств происходят не так часто, банк оценивает максимальный размер неординарных отклонений, который будет превышен лишь с некоторой заданной вероятностью. Априорно устанавливая уровень вероятности, банковское учреждение определяет для себя степень риска, на которую он готов пойти в процессе управления банковской ликвидностью.
- Прогнозирование остатка средств на счете до востребования. Специалистами Национального банка Республики Беларусь предложено рассматривать следующие варианты событий:
- если динамика остатка средств на счете до востребования не имеет частых значительных списаний, то для определения стабильного остатка средств можно использовать ARIMA-модель и ограничиться в этом случае доверительным прогнозным интервалом, построенном на основе оценки данной модели;
- если наблюдаются частые значительные внезапные колебания остатков на текущем счете, то условно-постоянная их часть будет соответствовать их текущему значению за минусом вероятного значения объема интервенции (неординарного отклонения) для установленного банком доверительного интервала [4, с. 20];
- если банк исходит из случая одновременного наступления предыдущих двух событий, то в качестве условно-постоянного остатка на счете до востребования предлагается использовать величину, равную разности спрогнозированного с помощью ARIMA-модели значения минимального остатка на счете и оценки возможной интервенции для установленных соответствующих доверительных интервалов этих двух событий.
Анализ предложенного учеными С. Толочко и Н. Мирончук научно-методического подхода по прогнозированию условно-постоянного остатка на текущих счетах клиентов позволяет сделать следующие выводы:
- Описанный подход, по мнению самих ученых, может использоваться при управлении активами как коммерческими, так и центральными банками (например, в рамках управления ликвидностью золотовалютных резервов).
- В рамках своего научного исследования ученые не рассматривали характер колебаний совокупных остатков средств до востребования, а сосредоточили свое внимание на довольно волатильных остатках средств на отдельном текущем счете. По нашему мнению, при управлении ресурсами в практике банковского менеджмента текущие пассивы рассматриваются преимущественно как совокупность остатков по текущим счетам клиентов, клиенты не выделяются в зависимости от величины и динамики остатков на счетах (кроме VIP-клиентов). Экономический эффект при учете совокупных остатков средств депозитов до востребования проявляется в более высоких потенциальных объемах средств условно-постоянной части текущих пассивов, которые банк может трансформировать в кредитно-инвестиционные ресурсы.
- Ученые не уточняют критерии выделения значительных внезапных списаний по счету, а также предельную их частоту для выбора банком соответствующего способа расчета условно-постоянной части средств до востребования.
- Рассмотренный подход, в целом, можно взять за основу для определения условно-постоянной части совокупных депозитов до востребования банка при условии проверки гипотезы на однородность дисперсии, отсутствия кластеризации ее волатильности (внезапные изменения в виде оттока или притока средств не «затухают», а продолжаются еще некоторое время), что, в свою очередь, может потребовать пересмотра научно-методического инструментария: использование ARCH/GARCH-моделей как дополнение к ARIMA.
С учетом выявленных особенностей рассмотренных научно-методических подходов для определения совокупной величины условно-постоянной части депозитов до востребования предлагаем дальнейшие развитие научного инструментария в решении данной проблемы. Рассмотрим ежедневные совокупные остатки депозитов до востребования юридических лиц на примере одного из севастопольских банковских учреждений за период в один календарный год с детализацией по рабочим дням (пятидневная рабочая неделя) (рис. 4).
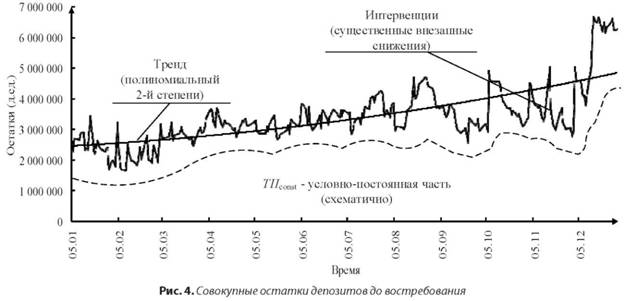
Анализ рисунка 4 позволяет выявить ряд особенностей в динамике анализируемого финансового временного ряда:
- На всем временном интервале совокупные остатки средств не опускались ниже 1600 тыс. денежных единиц и имели тенденцию нелинейного роста (тренд), что в условиях стабильной экономической конъюнктуры позволяет говорить о наличии в их динамике условно-постоянной величины.
- Остатки средств весьма волатильны и, по-видимому, имеют сезонную составляющую.
- Наличие явной тенденции и сезонности в динамике анализируемых остатков ограничивает возможность применения эвристических и чисто стохастических моделей (рис. 1) для определения условно-постоянной части депозитов до востребования с достаточной степенью достоверности.
- Визуально выявленная волатильность остатков средств требует проверки гипотезы на неоднородность их дисперсии. В случае подтверждения данной гипотезы необходимо выбрать наиболее адекватную статистическую модель для определения величины депозитов до востребования, которые банковское учреждение сможет направлять в кредитно-инвестиционные проекты, не испытывая при этом существенных рисков ликвидности.
В процессе анализа динамики депозитов до востребования с использованием известных статистических приемов [4, с. 18] были выявлены и исключены из финансового ряда совокупные остатки средств (в общей совокупности 12 наблюдений), которые отличались неординарным «всплеском» и быстрым «затуханием» на протяжении одного-двух операционных дней.
Проверку гипотезы на волатильность дисперсии депозитов до востребования (рис. 4) проведем с использованием ARCH-метода. Все необходимые расчеты произведем в эконометрическом пакете EViews.
Принимая во внимание нелинейный характер в динамике депозитов до востребования (рис. 4), преобразуем подготовленный временной ряд (d) в ряд вторых разностей логарифмов его значений — Δ2log(d), что иллюстрирует рисунок 5.
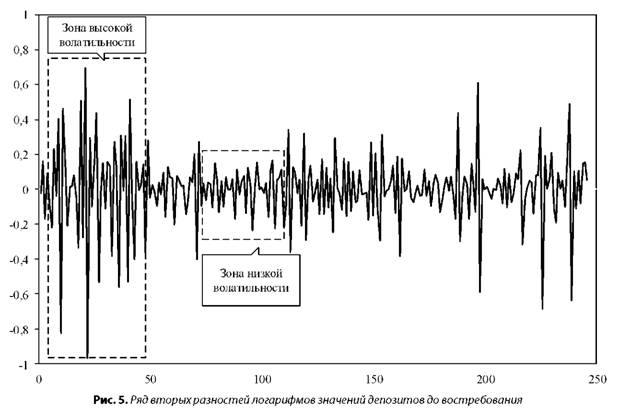
Далее была построена регрессия с параметрами Δ2log(d) и фиксированной константой, и протестированы остатки этой регрессии на ARCH-эффект. По результатам расчетов подтвердилась гипотеза о неоднородности дисперсии депозитов до востребования. Возвращаясь научно-методическому подходу С. Толочко и Н. Мирончук, подчеркиваем объективную необходимость предварительной проверки такой гипотезы. В случае ее подтверждения прогнозирование условно-постоянной части депозитов до востребования должно производиться с учетом выявленной волатильности их дисперсии.
Опуская подробное описание поиска наиболее подходящей модели прогнозирования депозитов до востребования, которая учитывала бы ARCH-эффект, приведем лишь конечный результат исследований. По анализируемым данным наилучшей интегрированной моделью авторегрессии скользящего среднего стала модель ARIMA(1, 2, 1):
Δ2log(d)t = - 0,112Δ2log(d)t-1 - 1,042εt-1, (13)
где Δ2log(d)t, Δ2log(d)t-1 — оцененные и фактические значения прологарифмированной величины депозитов до востребования в периодах t и t - 1 (с уровнем интегрирования, равным 2) соответственно;
εt-1 — значение ошибки модели в периоде t - 1.
Дальнейший анализ данных показал, что различная амплитуда колебаний совокупных остатков средств по счетам в разные периоды времени (кластеризация волатильности) может быть вызвана влиянием положительных и отрицательных рыночных шоков на хозяйственную деятельность клиентов банка. Данные шоки вполне могут быть связаны с той полнотой информации, которой располагают экономические субъекты (клиенты банка) относительно конъюнктуры рынка, финансового состояния контрагентов, покупателей. В конечном итоге, наличие асимметрии информации между субъектами экономических отношений приводит к различной реакции каждого субъекта на новую информацию («плохие», «хорошие» новости).
Анализ рисунка 5 подтверждает наличие асимметричного эффекта: на протяжении января-февраля банковское учреждение столкнулось с усилением колебаний совокупных остатков средств по счетам, что могло быть результатом негативных ожиданий клиентов относительно будущей макроэкономической ситуации в стране. Наилучшей моделью, которая смогла объяснить нелинейное изменение дисперсии ошибки в уравнении (13), стала EGARCH-модель (с экспоненциальным эффектом асимметричности [17]):
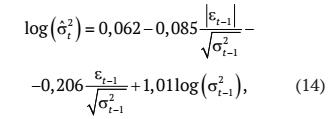
где σt2 — оцененная дисперсия ошибки εt.
Все оцениваемые параметры уравнений (13), (14) оказались статистически значимыми, а коэффициент детерминации составил 0,614. Предположение о нормальности распределения ошибки (εt) было отвергнуто, хотя плотность распределения их стандартизированных значений имеет форму, которая довольно близка к нормальному закону (рис. 6).
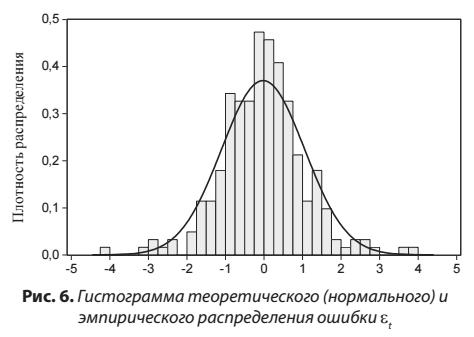
В этой связи необходимо отметить, что выводы, строящиеся на предположении о нормальности распределения ошибки, могут быть вполне обоснованными [18, с. 35]. Известно, что нормальный закон распределения является предельным, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. Поэтому анализ ежедневных сумм депозитов до востребования на больших выборках и выявление сезонных компонент финансового ряда, которые проявляются на уровне календарных лет (в нашем примере рассматривается только один год), вполне могут привести к подтверждению справедливости данного тезиса.
С использованием формул (13) и (14) предлагаем определять условно-постоянную часть депозитов до востребования — ТП) на основе следующего выражения:
TПconst(t) = dt - kσt, (15)
где dt — оцененное значение величины депозитов до востребования в периоде t;
k — величина нормированного стандартного отклонения, соответствующая заданному уровню надежности;
σt — оцененное стандартное отклонение ошибки εt.
Принимая во внимание асимптотическое приближение распределения ошибки εt к нормальному закону, установим значение параметра к на уровне 1,96, что будет соответствовать 95-процентному уровню надежности прогноза с учетом смоделированной дисперсии σt2. Следовательно, формулу (15) можно записать в виде:
TПconst(t) = dt - 1,96σt.
Иллюстрация условно-постоянной части депозитов до востребования на основании предложенного научно-методического подхода приведена на рисунке 7.
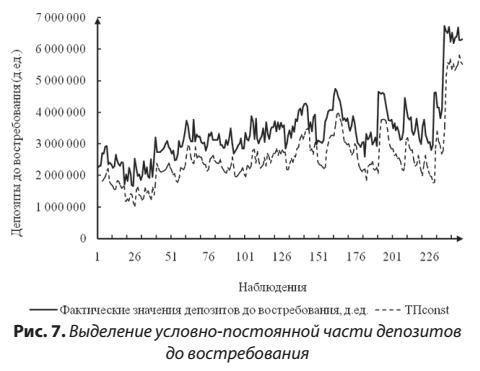
Выводы
Таким образом, предложенный научно-методический подход для определения условно-постоянной части депозитов до востребования, который предполагает построение их краткосрочного интервального прогноза, основан на поэтапной статистической обработке финансового ряда и выявления закономерностей в их динамике. По результатам исследования была подтверждена гипотеза о наличии асимметричных эффектов в распределении дисперсии депозитов до востребования. Эти эффекты вызваны положительными и отрицательными шоками, с которыми постоянно сталкиваются в своей хозяйственной деятельности клиенты банка.
Экономический эффект от применения предложенного научно-методического подхода состоит в более рациональном, в сравнении с проанализированными методиками (эвристическими, статистическими), использовании «дешевых» и, в то же время, нестабильных депозитов до востребования для финансирования долгосрочных активных операций банка. Определение уровня условно-постоянной части текущих пассивов с учетом возможной волатильности дисперсии совокупных депозитов до востребования, по нашему мнению, может оказать положительное влияние и на качество банковского планирования по использованию потенциала «коротких» ресурсов банка, что, в свою очередь, может быть предметом отдельных научных исследований.
Кроме этого, выявленные и смоделированные закономерности в изменении совокупных депозитов до востребования создают реальные условия для эффективного управления ликвидностью банка, ценообразования банковских ресурсов, что на мезо- и макроуровнях национальной экономики создает позитивные предпосылки для более активного вовлечения банковского сектора экономики в инвестиционные процессы.
Список источников
1. Вожжов А.П., Лунякова Н.А. Учет влияния депозитных рисков в процессах трансформации банковских ресурсов // Формування ринкової економіки в Україні. — 2009. — Вып. 19. — С. 16-26.
2. Вожжов А.П. Процессы трансформации банковских ресурсов. — Севастополь: СевНТУ, 2006. — 339 с.
3. Герасимова Е.Б. Анализ банковских ресурсов методом коэффициентов // Финансы и кредит. — 2003. — № 1. — С. 22-25.
4. Толочко Ю., Мирончик Н. Прогнозирование условно постоянного остатка на текущих счетах клиентов // Банкаусю весшк. — 2002. — № 16. — С. 17-21.
5. Карчева А.Т. Моделювання інвестиційної діяльності банків // Вісник Національного банку України. — 2004. — №10. — С. 11–15
6. Конюховский П.В. Микроэкономическое моделирование банковской деятельности. — СПб: Питер, 2001. — 224 с.
7. Лаврушин О.И. Банковское дело / О.И. Лаврушин, И.Д. Мамонова, Н.И. Валенцева и др. — М.: КНОРУС, 2009. — 768 с.
8. Масленченков Ю.С. Финансовый менеджмент в коммерческом банке: Кн.3: Технология финансового менеджмента клиента. — М.: Перспектива, 1997. — 214 с.
9. Панова Г.С. Анализ финансового состояния коммерческого банка. — М.: Финансы и статистика, 1996. — 272 с.
10. Тагирбеков К.Р. Основы банковской деятельности. Банковское дело. — М.: ИНФРА, Весь Мир. — М, 2003. — 720 с.
11. Сухарський В.С. Ощадна справа. Основи теорії і практики. — Тернопіль: Навчальна книга — Богдан, 2000. — 256 с
12. Иванча А.И. Оптимизация условно-постоянного остатка на счетах «до востребования» коммерческого банка // Управление экономическими системами. — 2011 [Электронный ресурс]. URL: http://www.uecs.ru/uecs-34–342011/item/722--l-r-(дата обращения: 11.02.2015).
13. Самойлов Е.В. Совершенствование методов управления мгновенной и краткосрочной ликвидностью коммерческого банка: автореф. дис. ... канд. эконом. наук. Нижний Новгород, 2006 [Электронный ресурс]. URL: http://www.1ib.ua-ru.net/diss/cont/197059.htm1 (дата обращения: 10.02.2015).
14. Шиллер Р.І. Оптимізація обсягів і структури залучених і запозичених коштів для досягнення фінансової стійкості банку // Фінанси України. — 1997. — №12. — С. 47- 53.
15. Лунякова Н.А. Депозитные риски в банковской деятельности. — Севастополь: Рибэст. — 2009. — 208 с.
16. Вентцель Е.С. Теория вероятностей. — М.: Наука. — 1969. — 576 с.
17. Nelson D. (1901). Conditional heteroskedasticity in asset returns: a new approach. Econometrica, 50, 347-370.
18. Андерсон Т. Статистический анализ временных рядов. — М.: Мир, 1976. — 756 с.
Скачать ФинЭкАнализ
Попробовать ФинЭкАнализ
