Сравнительный анализ значений внутренней нормы доходности инвестиционного проекта, полученных по различным методикам расчета
Коростелева М.В.
к.э.н., доцент кафедры экономической кибернетики
Санкт-Петербургского государственного университета,
Санкт-Петербург, Российская Федерация
Иннов: электронный научный журнал
№4 (33) 2017
Аннотация: Статья посвящена исследованию методов расчета внутренней нормы доходности инвестиционного проекта - одного из критериальных показателей, используемых при анализе эффективности капиталовложений. При выборе из нескольких альтернативных инвестиционных проектов инвестора, как правило, больше интересует значение внутренней нормы доходности, рассчитанное с учетом налогообложения, нежели значение, вычисленное до вычета налога на прибыль. Поэтому в статье рассматривается вопрос о том, как влияют налоговые выплаты на погрешность при расчете внутренней нормы доходности по различным формулам. В связи с этим целью статьи является оценить значение внутренней нормы доходности инвестиционного проекта, описываемого денежным потоком до налогообложения и после него. В статье анализируется соотношение между значениями внутренней нормы доходности, полученными с использованием методов приближенных вычислений, и ее фактическими значениями в условиях, когда компоненты денежного потока инвестиционного проекта определяются с учетом налога на прибыль. В статье проводится сравнение двух методов определения ставок, и показывается необходимость и возможность использования того и другого метода. Отмечается, что разница между внутренней нормой доходности, вычисленной по методу приближенных вычислений, и ее фактическим значением, невелика, и во многих случаях использование метода приближенных вычислений, вероятно, не приведет к серьезным ошибкам в принятии решений. Показывается возможность использования метода приближенных вычислений на практике, но указывается необходимость учета того факта, что использование этого метода дает заниженную оценку внутренней нормы доходности инвестиционного проекта.
Введение
При анализе эффективности капиталовложений одной из задач является выбор такой формулы, используемой для отбора инвестиционных альтернатив, которая объединяла бы различные показатели инвестиционного проекта (инвестиционные затраты, срок реализации и пр.) в один, и тем самым обеспечивала бы относительную и абсолютную меру привлекательности проекта. Найти подобную формулу можно при помощи методов приближенных вычислений, широко распространенных в использовании при оценке эффективности реализации инвестиционных проектов. Однако возникает вопрос о соответствии результатов, полученных при помощи методов приближенных вычислений, и фактическими значениями показателей.
Материалы и методы
Рассмотрим на примере одного из критериальных показателей, используемых при оценке инвестиционных альтернатив, а именно, внутренней нормы доходности проекта (IRR), основные соотношения между приближенным значением и фактическим значением IRR (подробнее о приближенных методах расчета внутренней нормы доходности см., например, [12]).
Для расчета внутренней нормы доходности (IRR) инвестиционного проекта по денежному потоку с учетом налоговых отчислений на практике часто используется следующее выражение [11, с. 255]:
r = (1 - N) * k, (1)
где k - внутренняя норма доходности по денежному потоку без учета налоговых отчислений,
N - ставка налога на прибыль.
Из выражения (1) можно приближенно определить значение внутренней нормы доходности инвестиционного проекта.
В данной статье мы исследуем соотношение между приближенным значением IRR, получаемым из выражения (1), и ее фактическим значением, r*, получаемым непосредственно в условиях, когда налоговые платежи включаются в поток расходов [19, 20, 21].
Определение соотношения между приближенным значением IRR и ее фактическим значением.
В предположении о том, что амортизация начисляется нелинейным способом, внутренняя норма доходности без учета налогообложения, k, вычисляется путем решения следующего уравнения:

где CFo - инвестиционные затраты (первая компонента денежного потока с одинаковыми остальными компонентами CF),
T -плановый период инвестора, t = 1, 2,...,T.
Далее для упрощения расчетов будем предполагать, что налоговые платежи являются равномерными, тогда фактическое значение внутренней нормы доходности с учетом налогообложения, r*, получается путем решения следующего уравнения:

где амортизационные отчисления Dt изменяются от года к году в соответствии с формулой:
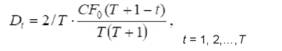
В случае начисления амортизации линейным способом IRR без учета налоговых отчислений может быть выражена следующим образом:

откуда получаем

Компоненты денежного потока с учетом налогообложения определяются как (1 - N) * (CF - D) + D, где D - размер равных ежегодных амортизационных отчислений, равный CF0/T,
Поэтому справедливо следующее равенство:
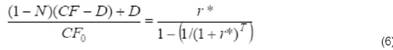
Поскольку D/CF0 = 1 / T,
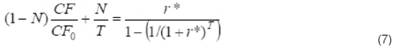
Из уравнений (5) и (7) можно определить соотношение между приближенным значением IRR до налогообложения и ее фактическим значением после налогообложения:
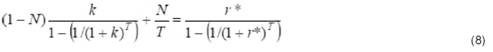
Результаты и обсуждение
В табл.1 представлены расчетные значения соотношений r*/r для разных приближенных внутренних ставок после налогообложения и для разных значений планового периода инвестора, а на рис. 1 - график зависимости соотношений r*/r от значений планового периода. Ставка налога на прибыль равна 20%, ее изменение не предполагается.
Таблица 1. Соотношения между фактическим значением IRR с учетом налога и ее приближенным значением в случае равномерной схемы начисления амортизации.
| Ставка | 10% | 20% | 30% | 40% |
| Срок, лет | ||||
| 1 | 1,00 | 1,00 | 1,00 | 1,00 |
| 2 | 1,00 | 1,01 | 1,01 | 1,01 |
| 3 | 1,00 | 1,01 | 1,01 | 1,02 |
| 5 | 1,01 | 1,02 | 1,02 | 1,03 |
| 7 | 1,02 | 1,02 | 1,03 | 1,03 |
| 10 | 1,02 | 1,03 | 1,04 | 1,04 |
| 20 | 1,03 | 1,04 | 1,03 | 1,03 |
| 30 | 1,04 | 1,04 | 1,03 | 1,02 |
| 40 | 1,04 | 1,03 | 1,02 | 1,02 |
| 50 | 1,04 | 1,02 | 1,02 | 1,01 |
| 60 | 1,04 | 1,02 | 1,01 | 1,01 |
| 70 | 1,03 | 1,02 | 1,01 | 1,01 |
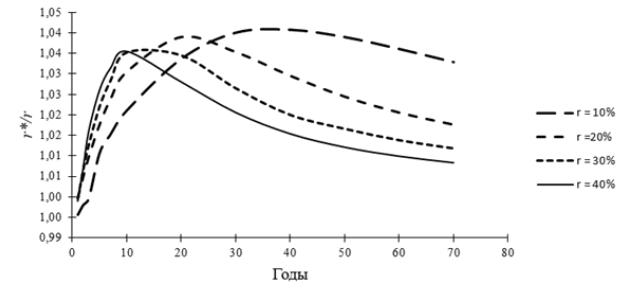
Рисунок 1. Зависимость соотношение ставок от планового периода
В случае равенства ставок, т.е. когда r*/r = 1, значения «посленалоговой» внутренней нормы доходности, оцененной по методу приближенных вычислений, совпадает с ее фактическим значением. Чем больше отклонение соотношения ставок от единицы, тем менее точной является оценка. Вычисления по методу приближенных вычислений всегда приводят к заниженному значению IRR. Так, например, для комбинации значений k = 20% и T = 20 оцененная по методу приближенных вычислений с учетом налогообложения ставка равна 16%, тогда как фактическое ее значение равно 16,62%, т.е. метод приближенных вычислений «может привести к отклонению фактически выгодных проектов, однако не может привести к принятию фактически невыгодных проектов» [12, с.164]. По мере увеличения планового периода инвестора соотношение ставок также увеличивается до определенной точки, а затем снижается, однако снижение происходит уже в области, где соответствующие значения IRR и планового периода являются далекими от реальной действительности.
Выводы
Подводя итоги, можно сказать, что разница между внутренней нормой доходности, вычисленной по методу приближенных вычислений, и ее фактическим значением, невелика, и во многих случаях использование метода приближенных вычислений, вероятно, не приведет к серьезным ошибкам в принятии решений. В то же время необходимо заметить, что этот вывод относится к случаю, когда компоненты денежного потока до налогообложения и амортизационных отчислений одинаковы в каждый год. Очевидно, более существенная разница между ставками будет возникать в результате неравных поступлений, несоответствия между сроком реализации проекта для целей налогообложения и действительностью и пр. Поскольку метод приближенных вычислений является более простым, представляется возможным его использование на практике, хотя при принятии решений очевидна необходимость учета того факта, что использование этого метода дает заниженную оценку внутренней нормы доходности инвестиционного проекта.
Библиографический список
1. Алексанов Д.С., Кошелев В.М. Экономическая оценка инвестиций. - М.: Колос-Пресс, 2002. - 382с.
2. Анализ и оценка эффективности инвестиций: учебник для студентов высших учебных заведений, обучающихся по экономическим специальностям / Т.У. Турманидзе. - М ЮНИТИ-ДАНА, 2014. - 247с.
3. Брейли, Р. Принципы корпоративных финансов. - М: ЗАО "Олимп-Бизнес", 2010. - 977с.
4. Виленский П.Л., Лившиц В.Н., Смоляк Н.А. Оценка эффективности инвестиционных проектов: Теория и практика: Учебно -практическое пособие. - М.: Дело, 2002. - 888с.
5. Воронцовский А.В. Инвестиции и финансирование: методы оценки и обоснование. - СПб: Изд-во СПбГУ, 2003. - 528с.
6. Воронцовский А.В. Методы обоснования инвестиционных проектов в условиях определенности - СПб.: ОЦЭиМ, 2010. - 228с.
7. Инвестиции: учебное пособие для студентов, обучающихся по специальности "Финансы и кредит" / М.В. Чиненов [и др.]. - М.: Кнорус, 2010. - 365с.
8. Инвестиции: учебник / А.Ю. Андрианов [и др.] - М ПРОСПЕКТ, 2010. - 584с.
9. Инвестиционный менеджмент: учебник по специальности "Менеджмент организации" / Н.Д. Гуськова [и др.]. - М.: Кнорус, 2010. - 451с.
10. Ковалев В.В. Финансовый менеджмент: теория и практика. - М.: ТК Велби, Изд-во Проспект, 2007. - 1024с.
11. Коростелева М.В. Расчет внутренней нормы доходности инвестиционного проекта с учетом налоговых отчислений // Научно-технический прогресс: актуальные и перспективные направления будущего. Сборник материалов VI Международной научно-практической конференции (18 августа 2017 года), Том II - Кемерово: ЗапСибНЦ, 2017. - С. 255-256.
12. Коростелева М.В. Использование методов приближенных вычислений для расчета внутренней нормы доходности инвестиционного проекта // Применение математики в экономике. Вып.17: Сборник статей / Под ред. А.В. Воронцовского. - СПб: Изд-во СПбГУ, 2009. — С.152-165.
13. Кремер Н.Ш. Математика для экономистов: от Арифметики до Эконометрики - М.: Юрайт, 2010. - 646с.
14. Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование. Учебное пособие. -М.: Вузовский учебник, 2007. - 365с.
15. Ример М.И., Касатов А.Д., Матиенко Н.Н. Экономическая оценка инвестиций. - СПб: Питер, 2008. - 480с.
16. Староверова Г.С. Экономическая оценка инвестиций. - М.: Кнорус, 2010. - 309с.
17. Хиггинс, Р.С. Финансовый менеджмент: управление капиталом и инвестициями. - М.; СПб.; Киев: Вильямс, 2013. - 463с.
18. Экономическое моделирование в Microsoft Excel / Мур Дж., Уэдерфорд Л.Р. и др. - М.: Издательский дом «Вильямс», 2004. - 1024 с.
19. Эртель А.Г. Зарубежный опыт функционирования инвестиционных фондов и его влияние на действующее в России законодательство // Современная научная мысль. 2014. № 2. С. 113-118.
20. Губанова Е.В. Опыт реализации мер по повышению инвестиционной привлекательности в условиях современной геополитической обстановки на уровне региона. В книге: Теоретико-методологические подходы к формированию системы устойчивого развития предприятий, комплексов, регионов Бондаренко В.В., Танина М.А., Юдина В.А., Кудинкин Р.С., Медушевская И.Е., Горячев Д.С., Мира Б.А., Полякова М.А., Вильгута О.Ф., Рудык Н.В., Губанова Е.В., Смолич Н.Г., Ушанова Н.А., Барбарская М.Н., Никишкина А.А., Пешкова К.С., Хорошилова Е.А., Гудович Г.К., Коротина Н.Ю., Ларкина А.А. и др. Пенза, 2016. С. 69-82.
21. Киселева И.А., Симонович Н.Е. Риски инвестора с позиции психолога и экономиста // СтройМного, 2016. № 4 (5). URL: http://stroymnogo.com/science/economy/riski-investora-s-pozitsii-psikholo/
22. Capital Budgeting Valuation. Financial Analysis for Today's Investment Projects./H.K.Baker, Ph.English, NJ: Wiley, 2011, 530 p.
23. Gotze U., Northcott D., Schuster P. Investment Appraisal. Methods and Models, Berlin: Springer-Verlag, 2008, 391 p.
Скачать ФинЭкАнализ
Попробовать ФинЭкАнализ
