Максимизация ожидаемой прибыли консалтинговой компании методами динамического программирования
Ариничев Игорь Владимирович
к.э.н.
Ариничева Ирина Владимировна
д.б.н., доцент
Кубанский государственный аграрный
университет, Краснодар, Россия
Политематический сетевой электронный научный журнал
Кубанского государственного аграрного университета
№115 2016
В данной статье, в соответствии с методологией динамического программирования, предложена методика распределения специалистов консалтинговой компании между ее проектами, с целью максимизации ожидаемой прибыли. Для ее реализации формируется математическая модель с нелинейной целевой функцией и линейными ограничениями. Нелинейность целевой функции обусловлена спецификой деятельности консалтинговых предприятий и их размером. В модель входят вероятностные параметры, определяемые методом экспертных оценок основываясь на предыдущем опыте работы фирмы на аналогичных работах и характеризующие успешность реализации каждого проекта входящего в портфель компании. Далее, рассматривается параметр и функция состояния, удовлетворяющие рекуррентному соотношению и производится линейная замена, чтобы зарезервировать минимальное количество специалистов на каждую работу. В работе приводится гипотетический пример консалтингового предприятия, включающего в свой портфель пять проектов с указанными прибылями в случае их успешного исхода и на его основе реализуется разработанная методика в виде 5-шаговой процедуры моделирования неизвестных параметров. Оценивается экономический эффект от применения данной методики. Разработанные модель и методика могут использоваться специалистами в консалтинговых компаниях, а также на предприятиях сферы услуг
В странах с развитой рыночной экономикой консалтинговые услуги являются важнейшим элементом поддержания ее инфраструктуры. В России данный рынок относительно молод, если сравнивать его с аналогичным рынком на Западе, однако уже обладает сформировавшимися взглядами, крупными игроками и конкурентной борьбой. В условиях постоянного экономического кризиса развитие консалтинговых услуг замедлилось. Компании данной отрасли испытывают те же трудности, что и их клиенты. Очередной ежегодный рэнкинг ведущих консалтинговых групп, подготовленный рейтинговым агентством RAEX, выявил застой на этом рынке. Сокращение бюджетов на консалтинг привело к уменьшению средней стоимости заказа, что в свою очередь обостряет ценовую конкуренцию между игроками рынка. В результате часть компаний вынуждена уйти с рынка, часть заморозить свою деятельность. По оценкам экспертов «рынок консалтинга колеблется на границе между застоем и сжатием» [6].
Поддержку своему бизнесу консультанты ждут в основном от проектов, реализуемых государством, и в меньшей степени от бизнеса, стремящегося в кризис снизить издержки. Так в соответствии с Федеральным Законом РФ [1] в ближайшее время на федеральном, региональном и муниципальном уровнях должны быть разработаны стратегии, координирующие процессы целеполагания, прогнозирования, планирования и программирования социально-экономического развития Российской Федерации, субъектов Российской Федерации и муниципальных образований. Учитывая колоссальный объем работ, для реализации данных проектов могут быть привлечены консалтинговые компании.
Чтобы сохранить долю рынка и выжить в тяжелой конкурентной борьбе, в числе прочего, компаниям консультантам необходимо рационально распределять имеющиеся ресурсы, формировать портфели проектов, оптимизировав, таким образом, свою деятельность.
Цель данной работы - предложить методику максимизации, ожидаемой прибыли консалтинговой компании, основанную на оптимальном распределении консультантов между проектами компании.
Предположим, что на предприятии имеется m консультантов-экспертов, которых нужно оптимальным образом распределить между n проектами, входящих в портфель данной компании. С каждым проектом будем ассоциировать вероятность успеха его реализации p,, которая является нелинейной функцией от числа занятых на проекте экспертов. Нелинейность зависимости является естественным ограничением. Например, если на проекте уже задействовано 50 человек, то еще один консультант, за редким исключением, вряд ли изменит вероятность успеха так же, как если бы на работу изначально было поставлено 5 человек. В данном ситуации прослеживается аналогия с принципом убывающей предельной полезности.
Графически зависимость между вероятностью успеха и количеством специалистов можно представить в виде кривой, изображенной на рисунке 1.
Уравнение кривой (рис. 1) задается как отношение

где λ - постоянный параметр, назначается для каждого проекта и определяется на основе экспертных оценок с учетом предыдущего опыта компании на аналогичных работах.
Из формулы (1) следует, чем больше значение λ, тем меньше вероятность успешной реализации рассматриваемого проекта. В пределе при λ → ∞ (k - фиксировано) вероятность успеха приближается к нулю. В противном случае, если λ=0, то p=1 (успешное выполнение достоверно).
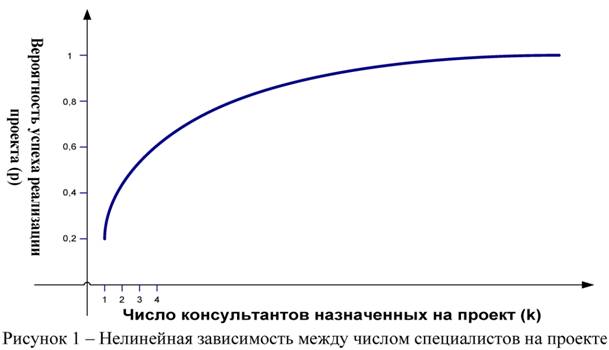
консалтинговой компании и вероятностью его успешной реализации
Кроме этого, с каждой работой i, в случае ее успешной реализации, будем связывать прибыль πi. Тогда задача распределения сотрудников консалтинговой компании формулируется следующим образом: требуется найти вектор u = (u1, u2,..., un), условиям
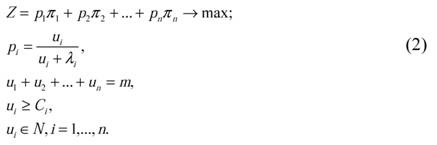
Целевая функция Z здесь представляет собой ожидаемую прибыль консалтинговой компании, после распределения всех экспертов. Второе уравнение, входящее в ограничение (2), определяет совокупность вероятностей, рассмотренных выше (см. (1)). Равенство три и неравенство четыре есть ограничения на число сотрудников: общее их число должно быть равно m (все имеющиеся специалисты должны быть задействованы) и на каждую работу не может быть сопоставлено консультантов меньше Ci>0. Последнее условие есть ограничение на целочисленность переменных.
Задача (2) представляет собой задачу целочисленного нелинейного программирования, которая может быть решена методами динамического программирования. В первую очередь произведем замены переменных νi = ui - Ci, чтобы зарезервировать на каждую работу не менее Ci специалистов. Тогда задача (2) преобразуется к виду
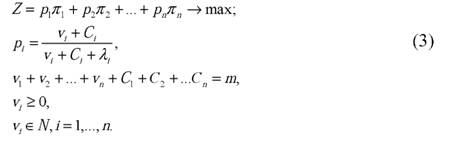
Введем параметр состояния и определим функцию состояния. За параметр состояния x примем количество сотрудников, выделяемое нескольким проектам, а функцию состояния Fk(x) определим как максимальную ожидаемую прибыль на первых k проектах, если им вместе сопоставлено x сотрудников, где после замены переменных x∈{0,1,...,15}. Можно показать [5], что функции Fk(x) удовлетворяет рекуррентному соотношению:
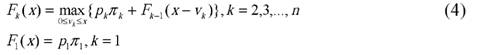
В начале процесса состояние системы нам известно, и делать какие-то предположения не нужно. Поэтому, имея в виду, что все последующие шаги спланированы для различных состояний системы, остается выбрать управление на первом шаге так, чтобы оно было оптимальным с учетом всех управлений, уже принятых наилучшим образом на всех последующих шагах.
Рассмотрим гипотетический пример, в котором консалтинговая компания сформировала портфель из пяти проектов управленческого консалтинга для различных бизнес-структур (n=5):
- обеспечение эффективного слияния;
- построение оптимальной системы документооборота;
- анализ и оптимизация действующей бизнес-модели;
- анализ регионального рынка сырья;
- построение эффективной маркетинговой стратегии.
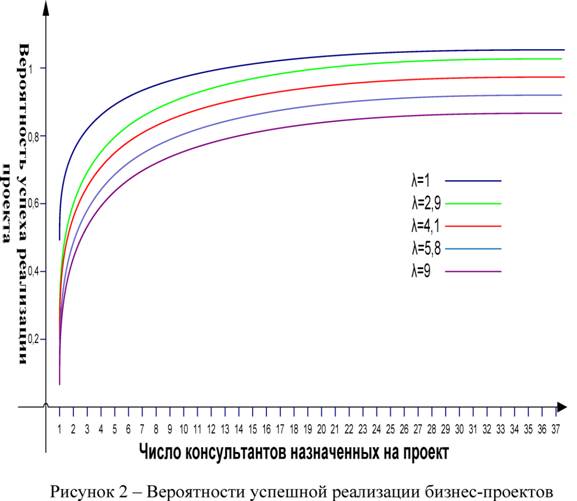
В общей сложности для реализации указанных проектов предприятие располагает сорока специалистами (m=40). На основе экспертных оценок были получены значения вероятностных параметров λi (соответственно списку) (см. рис. 2). Также будем считать, что на каждый проект должно быть сопоставлено не менее 5 сотрудников (Ci=5).
Рассмотрим случай, когда все специалисты компании поровну распределены между пятью проектами (Таблица 1).
Таблица 1 - Показатели бизнес-проектов консалтинговой компании до оптимизации
| Наименование проекта | Количество назначенных экспертов | Параметр λi | Вероятность успеха pi | Прибыль в случае успеха, руб. | Ожидаемая прибыль |
| Обеспечение эффективного слияния | 8 | 1 | 0,889 | 1500000 | 1333500 |
| Построение оптимальной системы документооборота | 8 | 2,9 | 0,734 | 1650000 | 1211100 |
| Анализ и оптимизация действующей бизнес-модели | 8 | 4,1 | 0,661 | 1180000 | 779980 |
| Анализ регионального рынка сырья | 8 | 5,8 | 0,58 | 470000 | 272600 |
| Построение эффективной маркетинговой стратегии | 8 | 9 | 0,47 | 250000 | 117500 |
| Всего | 40 | - | - | 3417680 |
В четвертой колонке таблицы 1 отображаются результаты оценивания вероятности успеха каждого проекта (1), с учетов параметров X; при k=8. В пятом столбце показана примерная прибыль компании в случае успешного исхода проекта. Умножив эти числа на ожидаемые вероятности успеха, мы получим значения последней колонки - ожидаемую прибыль.
Для максимизации суммарной ожидаемой прибыли рассмотрим задачу (4). Для ее решения нами были получены значения функций состояния Fi(x) и искомых параметров ν(x), i = 1,...,5 при каждом x∈{0,1,...,15}. В таблице 2 указаны значения величин νi(x) на каждом шаге
Таблица 2 - Результаты распределения специалистов компании
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| v1(x) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| v2(x) | 0 | 0 | 1 | 1 | 2 | 2 | 3 | 4 |
| v3(x) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| v4(x) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| v5(x) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| x | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| v1(x) | 8 | 9 | 10 | 11 | 12 | 13 | 15 | 15 |
| v2(x) | 4 | 5 | 5 | 6 | 6 | 7 | 7 | 8 |
| v3(x) | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 |
| v4(x) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| v5(x) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Из таблицы 2 видно, при x=15, количество сотрудников, сопоставленных пятому проекту равно v5(15)=0. На долю оставшихся четырех проектов по-прежнему остается 15 консультантов. На четвёртый проект должно быть выделено v4(15)=0 консультантов. Продолжая процесс было найдено v3(15)=3, v2(12)=6, v1(6)=6. Возвращаясь к исходным переменным по формулам ui = νi + Ci, окончательно находим: u1=11, u2=11, u3=8, u4=5, u5=5.
Вычислим ожидаемое значение прибыли для найденного (оптимального) распределения (таблица 3)
Таблица 3 - Показатели бизнес-проектов консалтинговой компании после оптимизации
| Наименование проекта | Количество назначенных экспертов | Параметр λi | Вероятность успеха pi | Прибыль в случае успеха, руб. | Ожидаемая прибыль |
| Обеспечение эффективного слияния | 11 | 1 | 0,916 | 1500000 | 1374000 |
| Построение оптимальной системы документооборота | 11 | 2,9 | 0,791 | 1650000 | 1305150 |
| Анализ и оптимизация действующей бизнес-модели | 8 | 4,1 | 0,661 | 1180000 | 779980 |
| Анализ регионального рынка сырья | 5 | 5,8 | 0,463 | 470000 | 217610 |
| Построение эффективной маркетинговой стратегии | 5 | 9 | 0,357 | 250000 | 89250 |
| Всего | 40 | - | - | 3765990 |
Сравнивая значения ожидаемой прибыли до и после оптимизации, замечаем, что экономический эффект составил более 340 тыс. руб., что говорит о неэффективном (см. табл. 1) исходном распределении экспертов предприятия между всевозможными работами.
Напоследок заметим, что представленная в работе методика максимизации ожидаемой прибыли консалтинговой компании не учитывает профессиональных особенностей каждого сотрудника в отдельности. Мы предполагали, что все специалисты обладают одинаковыми профессиональными навыками и опытом, а также, что каждый из них может быть поставлен на любую работу. Конечно, на практике это не всегда выполнимо. Снятие указанных предпосылок и решение вытекающих из этого задач будет представлено авторами в последующих работах.
Список литературы
1. Федеральный закон от 28.06.2014 г. № 172 «О стратегическом планировании в Российской Федерации» // СПС Консультант Плюс
2. Ариничев И.В. Математическое и имитационное моделирование производственной деятельности консалтинговых предприятий: Дис.... канд. экон. наук. Ставропольский государственный университет, Ставрополь, 2010.
3. Ариничев И.В. Имитационная модель процесса приема и обслуживания заявок в консалтинговых компаниях / И.В. Ариничев, Е.А. Семенчин // Труды Кубанского государственного аграрного университета. -20102. -№22. -С. 7-13.
4. Гайдук В.И. Стратегическое планирование основного капитала на малых предприятиях / В.И. Гайдук, И.В. Ариничев, Э.Е. Такахо // Труды Кубанского государственного аграрного университета. -2012. -№6(39). -С. 54-58.
5. Смоленцев В.М. Моделирование конкурентоспособности агропредприятия с учетом качества производимой продукции / В.М. Смоленцев / / Известия Тимирязевской сельскохозяйственной академии. -2006. -№4. -С. 169-172.
6. Соловьев В.И. Методы оптимальных решений / В.И. Соловьев. - Москва: Финансовый университет, 2012. - 364 с.
7. Ханферян В. Консультант в стране советов [Электронный ресурс] // Российская газета. - 2015. - №6676 (19.05.2015). - URL: http://www.rg.ru/2015/05/20/consalting.html
Скачать ФинЭкАнализ
Попробовать ФинЭкАнализ